Temporal Side Channels I

Temporal Side Channels I

View the video recordings for this chapter

History

In 1995, at the age of 22, Paul Kocher released a paper called Timing Attacks on Implementations of Diffie-Helman, RSA, DSS and other systems .

Before it was published, he wrote about it in a mailing list of Cypherpunks¹ which included all sorts of people like mathematicians, photographers, artists anarchists and more. The attack was first demonstrated in 1997 at a cryptography conference. And later, in 1998 an academic paper was published describing how to perform the attack. In 2003 and 2007 this kind of attack was used to break SSL.

The Threat Model

The objective of the attacker is to discover the password. The attacker goes about this by sending unlimited queries and measures their time. Unlimited queries are not always possible. Some devices are disabled after three to five tries. The same applies to time measurements. However the assumption is that these are possible according to Kerckhoffs’s principle(law), that states that everything except the key is public knowledge.

Figure 1.1 describes the Threat Model on an implementation of a secure system. It is important to mention that we’re talking about attacking an implementation, and not the algorithm itself as we consider the algorithm or protocol being examined as completely secure.

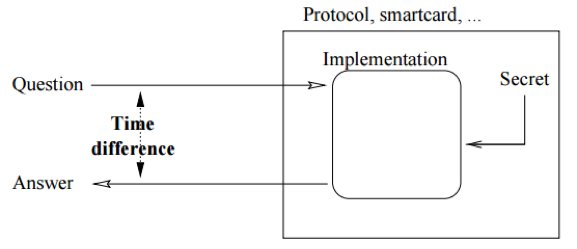
The Threat Model. Image from JF Dhem1998. The attacker can send a message to the implementation and get an answer from it. Also - the attacker is able to measure the time it takes for the implementation to compute the output

When is a timing attack even possible?

Physical access to the device. (for example: Smart card, Crypto wallet, Electronic voting machines)
Sharing a virtual machine with the service (for example: Swiping a credit card)
Remote access to a device (access to a device over the network, which may be very noisy and may be rather difficult to implement)

Timing attack

A timing attack is based on the time it takes to complete an algorithm.

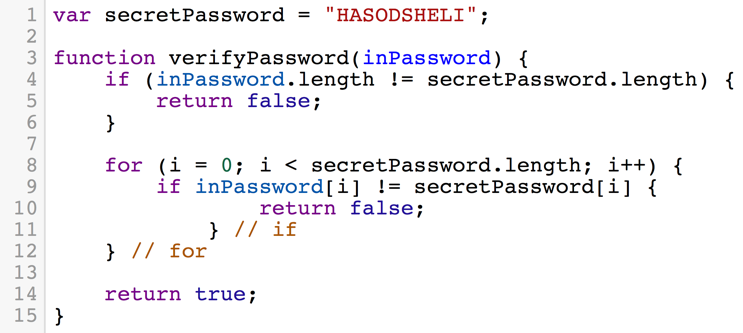
A simple and efficient password checking algorithm. In line 4 there’s a check if there length of the password is the same as the length of the input. In line 8 there’s an iteration over all of the characters in the password

Consider the algorithm for password checking as described in figure 1.2

In a scenario where a timing attack is not possible, breaking the password requires the attacker to bruteforce the password, checking every possible string for one successful attempt.

Let’s assume the password is the length of 16 characters, and if the password only contains english upper-case characters we have 26 possible values for each of the 16 characters in the password. The first character has 26 possiblites, the second has 26 possiblites and so on. So bruteforcing a password like this requries 26¹⁶ different attempts, which cannot be completed by any computer in a decent amount of time. In general, for a password of length n and character range of size k, breaking the password will take O(kⁿ) attempts.

Now let’s consider the scenrio where a timing attack is possible. To perform a timing attack, the attacker takes advantage of the fact that when the program checks for strings equality, the comparison will finish as soon as it finds one character that doesn’t match. Consider the following example where the attacker tries the 3 following attempts and measures the time it takes for the machine to respond. The attacker tries “AAAA” and measures 0.2ms, then tries “BAAA” and measures 0.5ms lastly tries “CAAA” and measures 0.2ms again. The attack can be pretty sure that the first character is “B”. Now, checking the whole password does not require iterating of all possible combinations of strings of size n. All it takes is to iterate over all possible values of each character, say k, and repeat that n times. This results in a total runtime of k + k + k + … = n**k = O(n)

We can now break the password in a reasonable amount of time, even without knowing the length of the password we’re trying to crack.

Timing Attack Defenses

After discussing the potential of such attack, we now consider the possible mitigations we can implement on our system to prevent such attacks.

Mitigation

We can consider adding a random wait time after checking each one of the characters. The problem of course is that the whole process of checking for a valid password becomes slower. And of course, if the attacker can perform a lot of measurements on our system, since the noise is random, the attacker would be able to ignore it.

Prevention

The second type of countermeasure is prevention, making sure that our system is completely resistant to timing attacks.

Prevention Method 1: Padding

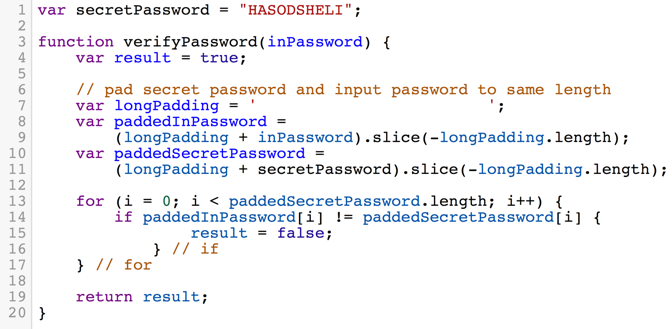
The first method we examine is to pad the secret password and the user’s guess to the same length. Also - the function dosen’t exit as soon as we see a character mismatch. The code is described in figure 1.3

The problem with this implementation is that every time there’s a character mismatch we execute additional code, which is loading the variable result and writing the value false to it. This may seem insignificant in the beginning but actually, this makes our code much more vulnerable than it was before. As now the time it takes for the entire function to complete is linearly dependant on the amount of characters mismatches we have, this allows an attacker to perform the same attack from before with no significant changes to his original timing attack.

One might think of a fix which is adding another branch to the if statement that will do some garbage operation like foo = false just so that the attacker might not be able to distinguish between a match and a mismatch. The problem with this fix might be that the access time to one variable may be different than the access time to another variable, and the attacker will be able to tell the difference between them.

Prevention Method 2: Hashing

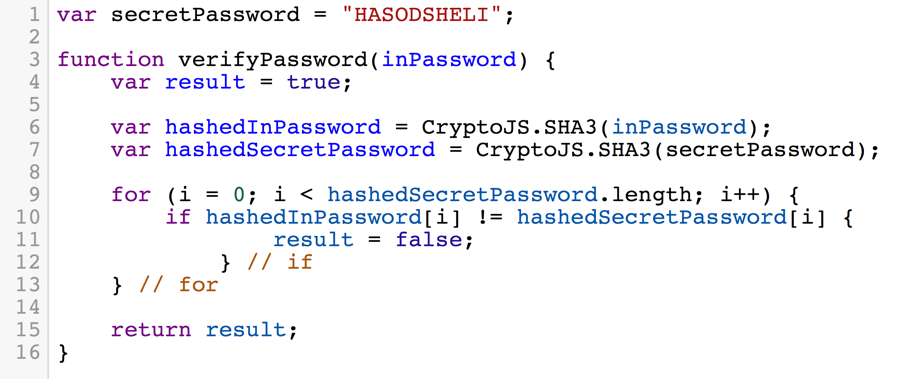
Secure password checking using a secure hash function

The right way to store passwords is with hashing (storing the hash of the password rather than the password in plain text). A hash is a cryptographic function which has the property called “The Avalanche Property” which means if even 1 bit is fliped in the input, at least half of the bits of the output are flipped as a result. This means that even if my guess is really close to the password (1 bit away from the real password) I cannot really know which bits are correct and which are not due to the Avalanche property.

Using hashes to perform a secure password check is described in the algorithm in figure 1.4 A guess is being hashed before it is compared against the hash of the true password. An attacker might use the same methods as described previously to try to leak the hash of the true password, but that would be very difficult as the attacker does not input the hash, the attacker only controls a string that is later being hashed by the algorithm. So trying the previous methods to leak the password would not work assuming the hash function is propely implemented.

A possible leak occuring from this method is the length of the true password. In line 7 of the algorithm in figure 1.4 the hash of the true password is computed. Line 7 makes the total run time of the program dependent upon the length of the true password. While this might be risky, this is easy to fix - we can just precompute the hash of the true password and use it whenever the algorithm runs. This is done for example in Linux where the hashes of user’s passwords are stored in a file in /etc/shadow.

The Algebra Behind RSA

The next thing we’re going to perform is a timing attack on the RSA crypto system. But before we dive into how we break RSA (next chapter) we’re going to discuss the algebraic foundation of RSA .

The RSA cryptosystem lives in something called a multiplicative group. The group that is Z_n^*.

We take 2 random prime numbers; p, q and assign n = p**q. The group Z_n^* contains all the numbers from 1 to n − 1 which do not divide n (that is, do not divide p or q). For example: for p = 3 and q = 5, n = 3 * 5 = 15 so Z_n^* = {1, 2, 4, 7, 8, 11, 13, 14}.

Like all groups, this group has the associative operation which in our case is the modular multiplication, that is because, as we mentioned before,this group is a multiplicative group. The group is also closed under that operation.

The group also has an identity element, 1. Which when multiplied by another element from the group - does not change it.

The last property this group has is that every element r in the group has an inverse element r⁻¹ ∈ Z_n^* so that r * r⁻¹ = 1.

Since the exponentiation is just repeated multiplication - we consider exponentiation to also be a closed operation under that group. Each element has an order, the order always divides (p−1)(q−1) (Fermat’s little theorem). When the element is raised to the power of the order, the result of the exponentation (under the modulu of course) is 1, the identity element in the group.

It also important to note that we cannot compute (p−1)(q−1) from knowing n

Elementary Operations of RSA

To use the RSA crypto system to encrypt and decrypt messages you first have to generate the infrastructure, that means deciding on p and q, both large prime numbers and computing n = p**q and (p−1)(q−1) denoted as ϕ(n)

Choosing a public and private key pairs Choose e ∈ Z_ϕ(n)^*, d ∈ Z_ϕ(n)^* such that e**d = 1 mod ϕ(n). The public key is the pair ⟨n, e⟩ and the private key pair is ⟨n, d⟩.
To encrypt a message Choose m ∈ Z_n^* as your message. The cipher is m^e mod n = c
To decrypt a message Since c = m^e mod n, perform c^d = m^e**d = m¹ = m mod n

Example: Consider p = 3, q = 5. So we can compute n = 3 * 5 = 15 and ϕ(15) = 2 * 4 = 8 Let’s assume we choose e = 3 and d = 11. We consider the message 2.

To encrypt, we compute 2³ = 8 mod 11, Which is the cipher.To decrypt, we’re using the private key 11 as follows: 8¹¹ = 2 mod 15. Now we have our message back, 2.

Since this is not a crypto course, we will not go into any more details about the algebra behind RSA. However it is important for us to familiarize ourselves with the basics of RSA in order to understand later how it was optimized and how can we break it.

Research Highlights

Timing and side channel attacks are well-known concepts in computer security and have been used to attack many kinds of systems, among those systems are cryptographic implementations, OpenSSL, SSH sessions, web applications and virtual machine environments. The following subsection will be devoted to showcase inspired works on some of the susceptible systems mentioned above. As mentioned at the beginning of the chapter, one of the pioneers to interduce these of attacks is Paul C Kocher in his paper . He described the ability of an adversary to find the private key of a cryptosystem by carefully measuring the amount of time required to perform private key operations. Another interesting work was done by D. Brumley et. al. who expanded the concept of timing attacks to apply for general software systems. Specifically, he and his colleagues devised a timing attack against OpenSSL. Through experiments they showed that they can extract private keys from an OpenSSL-based web server running on a machine in the local network. D. X. Song et. al. showed that using statistical techniques on timing information received through exploitation of two relatively minor weaknesses in SSH can lead to exfiltration of users typing in SSH session. In recent years, a wide variety of defense methods to protect both user space and kernel space code have been developed. As such, the attack surface of conventional exploitation strategies has been reducing significantly. Thus, both user space and kernel space code have become a target of timing side channels attacks. Hund et. al. presented that an adversary can implement a timing attack against the memory management system to deduce information about the privileged address space layout.