Temporal Side Channels Part 2

Temporal Side Channels Part 2

View the video recordings for this chapter

recap

In the previous chapter we discussed about RSA cryptosystem . In this chapter, we presented the most expensive operation in the RSA algorithm which is when we need to take the message (m) and raise it to the power of the key. C = m^e (mod n)) The simplest algorithm for raising a number to a power uses modular multiplication which is an expensive operation.

Modular multiplication is pretty straightforward. It works just like modular addition. You just multiply the two numbers and then calculate the standard name. Examples for Modulo 7 and 15 can be found in . Why modular multiplication is so expensive? Because we have to take the modulo many times which is as expensive as division¹. So, one way to do this is by keep multiplying and doing the modular reduction only at the end. The problem with that approach is that the runtime of multiplication grows exponentially with the number of the multiplicands. Another way is to do a mod**n with each multiplication, but the numbers keep growing and the runtime keep raising, so we can’t do that either.

Visualization of powers of 10 from one to 1 billion.

As we discussed in the last chapter, the slowest and most trivial way of implementing modular multiplication g^emod**n is to take g and multiply it by itself e times, and every once in a while do modulo n, (either every multiplication or just in the end). The problem with this is that if e is a number that consists of 1024 bits, then in the worst case we might need to multiply g in itself 2¹⁰²⁴ which is a huge number.

Efficiently Implementing Modular Exponentiations

There are two ways for efficiently implementing modular exponentiations:

performing fewer modular multiplications (instead of 2¹⁰⁰⁰ we would like to do 1000).
Make each modular multiplication to be less expensive.

The best case would be same as regular multiplication over integer. These two ways will reduce the cost of modular multiplication and modular exponentiations, and this is something we really want to do in order to make RSA work on a device.

So, assuming we are engineers, we want to implement modular exponentiations very cheaply. The right thing to do is obviously use some crypto library, but let’s assume that’s not possible, and we are inventing a new CPU. There is a very famous book online called the handbook of applied cryptography () . The book is like a recipe book, and is filled with algorithms, proofs and equations you need for cryptography. Chapter 14 deals with efficient algorithms for multiplicative proofs. The book contains several ways to do modular exponentiation.

Cover of the handbook of applied cryptography

The following approach is called the left to right binary exponentiation, also known as square multiply.

The pseudo-code was taken from the handbook of applied cryptography, page 615.

The inputs are g (we want to raise g to the power of e, g^e) and e which is a bit string of t (t bits), (see ). The most significant bit is always 1, because there is no logic behind raising something to the power of zero. In the end of this algorithm A will be the result of g raised to the power of e.

In the beginning we set A to be equal to 1, and go over the bits from left to right (from the most significant to the least). Each time we square A (A = A * A), but we only multiply by g (A=A*g) if the current bit is 1 (the i^t**h bit). Now, what happens when we do a squaring operation downstairs? What happens to the exponent upstairs? Its multiplied by 2. So g^e² = g^2e and g * g^e = g^e + 1. Now, we can think of a binary string, you can write down the bits using shifting (multiplying by 2 is shifting) and adding 1 is just putting one in the place.

So how many modular multiplications will be performed in order to raise g to the power of e? The answer is O(t). In the best case - what is the lowest amount of multiplications that will be performed? the answer is t + 1 as the first bit is 1 (most significant) so we do step 2.2 one time and all the rest of the bits are zeros, and so we will only do step 2.1 in these cases. In the worst cast - what is the highest amount of multiplications that will be performed? Answer: 2t, if all the bits equal to 1 we will do 2 multiplications for each bit (step 2.1 and step 2.2). In any case, this is equal to O(t), so instead of 2^t as in the old algorithm we perform at most 2t multiplications.

Lets review an example. Lets calculate 7⁶ = 7⁽¹¹⁰⁾ in the group ℤ₁₅ = 1, 2, 4, 7, 8, 11, 13, 14.

A = 1 = 7⁽⁰⁾
A = A * A = 1 = 7^(0<<1) = 7⁽⁰⁾
A = A * 7 = 7 = 7⁽⁰⁺¹⁾ = 7⁽¹⁾
A = A * A = 4 = 7^(1<<1) = 7⁽¹⁰⁾
A = A * 7 = 13 = 7⁽¹⁰⁺¹⁾ = 7⁽¹¹⁾
A = A * A = 4 = 7^(11<<1) = 7⁽¹¹⁰⁾

Are there any ways doing this even faster? The answer is yes as we can see in the handbook of applied cryptography. The general idea of these algorithms is that we do some pre-computation. The idea of RSA algorithm is that there is a public key g that is a known number. So if we know what g is we can prepare all sort of lookup tables. One method for doing that is called the window method, where we take three bits at a time, and instead of doing A * g we do A * g * g or A * g * g * g .. (8 values we can use), and instead of A = A * A we do A = A * A * A and so on, this is the sliding window. Another method is called the binary method, which is well described in the handbook of applied cryptography (page 616 algorithm 14.83). We can assume that any reasonable crypto implementation is not doing the naive method. It will use the left to right or the right to left binary exponentiation which is basically the same idea as one of the window methods.

But what if we want the modular multiplication to be cheaper? A way to achieve this is called the Chinese remainder theorem (CRT) , named after Sun-tzu Suan-ching that was a teacher from the century and wrote a book that contained all sorts of riddles and questions.

The Chinese remainder theorem addresses the following type of problem. One is asked to find a number that leaves a remainder of 0 when divided by 5, remainder 6 when divided by 7, and remainder 10 when divided by

The simplest solution is 370. Note that this solution is not unique, since any multiple of 5 × 7 × 12 (= 420) can be added to it and the result will still solve the problem. The theorem can be expressed in modern general terms using congruence notation. Let n1, n2, …, nk* be integers that are greater than one and pairwise relatively prime (that is, the only common factor between any two of them is 1), and let *a*1, *a*2, …, *ak be any integers. Then there exists an integer solution a such that a ≡ ai*(*modni*) for each *i* = 1, 2, …, *k*. Furthermore, for any other integer *b* that satisfies all the congruences, *b* ≡ *a*(*modN) where N = n1n2⋯n**k. The theorem also gives a formula for finding a solution. Note that in the example above, 5, 7, and 12 (n1, n2, and n3 in congruence notation) are relatively prime. There is not necessarily any solution to such a system of equations when the moduli are not pairwise relatively prime.

Why does this help us? Allegedly, we have to do 2 operations instead of one. The way to do exponentiations in CRT is that we take our big number and do modulo p and then modulo q and then there is a CRT step. So what is the size of the operand used by these two modular exponentiations? Assuming that p and q are of the same size? Let’s say p and q are 1000 bits so the size of n is 2000 bits (we add the number of bits of each number in the multiplication). So each number in the multiplicative group is about 2000 bits because it’s mod N, so multiplying two numbers is going to be multiplying two numbers which are 2000 bits. If we reduce it to modulo p and modulo q the numbers are going to be half the size (1000 bits). So if we take a multiplication and now we will multiply two numbers that are half the bit length what will be the speed improvement? It’s times 4. Instead of one big modular exponentiation we have one small modular exponentiation which costs quarter of the time and another one which cost quarter of the time followed by a CRT step which is a modular multiplication of the two. How much we spent in total? Answer: a bit more than half the time, twice speedup. Why can’t we do that further? Divide p and do it again? Answer: because p and q are prime numbers and that’s the whole point.

On top of that, there is a very nice trick, in order to make modular multiplications very cheap and this actually makes modular multiplications to be as cheap as regular multiplication. Multiply two numbers is pretty easy but the problem is reducing after multiplying. So what if there is a way of doing modular multiplications without the reduction step? So in 1985 a genius mathematician called peter Montgomery published a paper called “modular multiplication without a reduction step” ². The idea behind the paper is that we enter into a magical world called the Montgomery representation. When you step into the Montgomery world, modular multiplications do not require a reducing step and when you finish you just step out of this world and you are back with your result. It’s still cost you like a multiplication but it doesn’t cost you the extra reduction step. So, what is the idea of the Montgomery reduction? We want to calculate g^e (mod n) and to do that we need to pay a lot for modular reduction. So, the first thing we do is enter the Montgomery representation and do the Mont(g^e) and each one of this multiplication steps is going to be about as difficult as regular multiplication (Figure Figure 1.5). After we finished with that we exit the Montgomery representation and then we have our result. Entering and leaving the Montgomery representation costs as much as modular multiplication but in the middle it’s as cheap as regular representation.

General sketch of Montgomery Exponentiation

Now lets review how the Montgomery Exponentiation works inside

Choose a value R, R > n, which is easy to use (usually a large power of 2)
Mont*(*a*) = *a* * *R*(*modn)=^defa(mod**n)
$Mont(ab)=a*b*R(mod n)=\underline{a}*\underline{b}*R^{-1} (mod n)$
$= (\underline{a}*\underline{b} + (\underline{a}*\underline{b}*n’(mod R)*n))/R \pmod{n}$ // if this is more than n, subtract n
A = A * A = 4 = 7^(11<<1) = 7⁽¹¹⁰⁾
Result: Instead of modular reduction, we only (sometimes) subtract

The first thing to do is to choose a very large value R which is larger than n and should be easy to use (a large power of 2) for instance 1 and 1000 bits of zero. What does it mean easy to use? To multiply and divide by a power of 2 you just shift left and right. To calculate the modulo of a very large number that is a power of 2 you do bitwise and with this large power of 2. if R = 100000 and x = 10101010101110 so to do a modular reduction we just take the lower bits which are 01110 in this case. So we see it’s very cheap operation with R, but R is not useful outside the situation. So to enter the Montgomery representation we are going to multiply by R. This multiplication is modulo n, and this is a bit expensive. But how do we know that R is inside the multiplicative group? How do we know that multiplying by R doesn’t throw me outside of modn*? The answer is: how do we know that 2 is inside the group? Because what is this group? This group is a multiple of two prime numbers, and they are odd. Thus 2 doesn’t divide either one of them so 2 is in the group and 2 * 2 * 2…2 is in the group. We call the new number a. The idea is that the numbers in the Montgomery representation is cheap so how is it cheap with a If we multiply a and b in the Montgomery’s representation It will be: *a* * *b* * *Rmodn*. but if I want to do that using **a and b we get: $\underline{a}*\underline{b}R^{-1}$mod *n because of the extra R. So every time we multiply two numbers we need to take out the extra R. Inverting R is simple using GCD and can be done before we start the computation. There are much more derivations made to get to $(\underline{a}*\underline{b} + (\underline{a}*\underline{b}*n’(mod R)*n))/R \pmod{n}$. a*b is just a single multiplication. a*b*n’(mod R) - Notice that mod**R is a cheap operation because R is 1 with lot of zeroes. (n prime (n′) is just precomputed number that doesn’t really matter to us). Then we multiply it by n (another multiplication) and then we divide it by R which is also a simple operation. So, we have 4 multiplications and we need a modular reduction which is the main problem. Montgomery proofed that this sum is no more than 2ⁿ. So how do you do a reduction if the number is between 0 to 2ⁿ? You put an if statement. If x is less than n you do nothing, if x is larger than n you subtract it from the number n. So now, instead of division we do a couple of multiplications over integers which is not that expensive and then we sometimes subtract. This is a lot cheaper than the basic option and it is widely used. Notice that the if statement in the algorithm, which is influencing the execution time and might enable a timing attack.

Temporal Side Channel on RSA

Let’s review how to do a temporal side channel attack on RSA. Kocher described this attack on his paper in 1995 among other things. If the RSA runs slower than there are more subtractions and by timing the execution we can recover the key. So how this can be done? How to recover the key by timing the execution? There was a fantastic paper “A Practical Implementation of the Timing Attack” which the remainder of this section is based on. So what is the game here? Assume you are an attacker who wants to commit a timing attack on the secure implementation of RSA. If we have some device (e.g. a smart card) that we can send him requests, for instance “please allow to pay 1000 dollars to Alon” (see ). The smart card check that I have 1000 dollars in the bank account and then it replies “I approve this transaction and sign it”. So this card has stored a value inside which means he has money inside. On the other hand, we want that if we request “pay Alon 1 million dollars” the smart card will say “I don’t have enough funds! I am going to refuse”. As an attacker we would like to be able to sign any message we want, mainly messages like “please send Yossi 1 billion dollars”. The smart card will not allow it but if we got the private key (signing key) we can sign whatever message we want. So we send the smart card a message that is unsigned and he in return sends back a signature which is the response signed with the private key: m^s (mod n) where s is the secret key. We assume that as an attacker we can send as many queries as we want and we and recover the responses (the signatures). The goal is to extract the secret key.

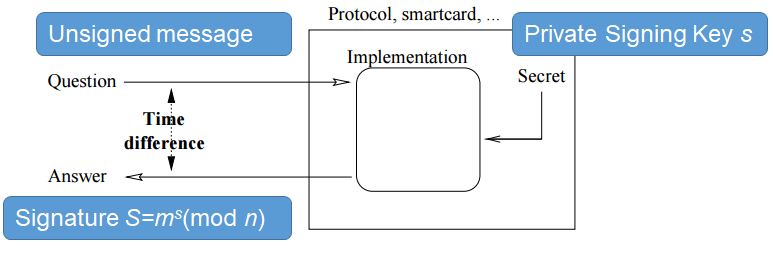
So, let’s look a bit closer on the attack model - what messages we can send to the smart card? Can we send any message we want? The answer is that we can only send valid messages - if the message is not valid then the smart card will just throw an exception. This is somewhere in the scale between the weakest model and the most powerful model. In this scenario the most permissive attack model is a known plain text. Known plain text means that we can see the messages as they are go in to the smart card but cannot change them. So the next thing is choosing the plain text. We can’t just chose any plain text, it has to follow a certain rule. The next thing is completely chosen plain text which doesn’t enforce any rules, and the last thing is adaptive plain text which means we can look at the response and we can choose the next query that we will send. So, what is the attack model, we send requests, the smart card is signing them, and we get the responses and also assuming that the smart card is using Montgomery RSA . So how can we use it to extract the key? We are going to use a method called “Vaizata” method which can be found in the DPA handbook. This is a general way of performing a side channel attack using statistics.

The “Vaizata" Method

Make a simple assumption about the implementation
Guess a little part of the key
Make hypothesis about the effect of the guess on the execution
Classify the measurements according to the hypothesis
If we guessed right, the classification will be statistically meaningful

How does it work? First, we make a simple assumption on the implementation, an assumption could be: We assume that the implementation run on software (the other possibility is hardware) what does it gives us? Software is executed serially and in the hardware it’s not the case. We can assume for example that the key is stored in a flash memory on the device, and every time we need to use the key then we need to read the flash memory. How can we find that this is the case? How can we find first of all that a device is on using the hardware or the software? One way is to look at it - we can open the screws and look with a microscope, or we can go to this wonderful website called “I fixed it”. They disassemble all sorts of devices and share this information. What is the sign that the device is using software? If there is an update on the firmware, because when it wakes up it needs to find out what software to run. We can say that this device uses memory, and we can also say things about when the device is doing the encryption. Let’s assume the device under test is a remote controller. Inside the controller there is a secret key stored and also a counter. Whenever the button is pressed the remote controller constructs a package containing the serial number of the controller, the counter and a boolean state of the button (which ever button was pressed). Then, it sends it to a car and the car decrypts it. Why do we need a serial number? Each ECU in the car has a program to accept remote controls. So why do we need the counter? Without the counter, an attacker can repeat a message sent from the remote controller to the car only by reading the messages and sending them again. What happens when you press the button and the car is in the train station? The counter in the remote controller is out of sync with the counter in the car ans there is a window of counter values the car will accept. If its closed, the car will open without complaining. If it’s a little closed we will need to press the remote control twice and when the car will see consecutive values and it will open, but if it is too far it won’t open. Let’s assume we can find out when the controller is transmitting (it is a very intensive operation that takes battery life and also radiates). So we know the moment in time when it is transmitting, did the encryption happened before or after the transmission? The answer is before. Let’s assume that the counter stored in the memory and let’s say we found the moment in time when the chip is reading from memory. Did it happen before or after the encryption? The answer is after, since we need the counter to be included in the message that will be sent. We can also make more assumptions such as “the AES uses an 8 bit data pack or 16 bit or 32 bit”. Some of these assumptions might be wrong but the “Vaizata” method will help us to find out if they are wrong.

So first of all we make a simple assumption, that the smart card is using left to right binary exponentiation using Montgomery and this is a very reasonable assumption because most implementations are using this method. The next thing to do is recursively (or inductively) guess a little part of the key. if we guessed the whole password it would take us exponential time but if we could guess a small part of the key each time it would take a linear time. So, we will try to guess small parts of the key first, and maybe the simplest thing to explain is guessing one bit or a single character, but lets say we are guessing a small part of the key. So now we know the beginning of the key and there is a little part we don’t know. The next step is that we need to make a guess about what kind of effect our guess is going to have on the computation. We can say, for example, that if we will guess the bit correctly then something will happen to the computation, and if we will guess this key bit correctly it will take more power/take longer time/connect to the network more often or some kind of other phenomena we can measure. So, in our case what is the only thing we can measure? Answer: The answer is time. We assume that if there is a Montgomery reduction in the calculation of this bit then the entire computation is going to take a little more time.

SO what is going on here? There is a very large computation here and we were able to guess the beginning of it but not the end of it. Now we are going to classify the measurements according to our hypothesis, in this case two groups (with or without Montgomery computation). If we guessed correctly then it will take longer to the group we said it will take longer. If not, it might take less or more, we can’t determine. If we guessed correctly, the groups will have meaning, means will be able to statistically tell apart the set of the measurements that will take a longer time and the set of measurements that will take less time. We are going to guess the left bit of the key, and there is only one option. The next bit can be 1 or 0. Now, we can simulate the running of this algorithm with our guess, not for the whole key but only to the part we know, and if there is going to be Montgomery reduction. So assuming we have g, e and N. The device under test is calculating g^e (mod n), but where g came from? It is supplied by the attacker. What about e? Secret we want to discover (e_t, e_t − 1, .., e₀) What about N? public variable (known). The first thing it does, it enters the Montgomery representation. This information of how to enter the Montgomery representation is known to the attacker. It starts with g, and then g becomes Mont*(*g*), but the attacker can also do it. First *A* = 1, then *A* = *A* * *A* the next thing is *A* = *A* * *g* because we know that the most significant bit is 1. The next step is *A* = *A* * *A*, now what is next? It depends, if *e*_{*t* − 1} = 0 then *A* = *A* * *A* (skipping to next bit). Else if *e*_{*t* − 1} = 1 then *A* = *A* * *g*. What happens next now we can’t know. We can run both calculations, in particular we can find out if there was a reduction step in two optional operations. There are 4 options: Only one of then containing a reduction step, two of them containing a reduction step or neither of them. We can know exactly, assuming we make a guess on *e*_{*t* − 1}, if there is going to be an extra reduction step. We know enough to guess - if we guess correctly, we can know if there will be a reduction step because we can calculate all the alternative options completely. So, let’s do this now, we have many different g’s, and we have repeated this step many times, and for each of these g’s we know if there is going to be an extra reduction step. So, now let’s see how we can do an attack using this information. So, there is private key *s*, a public key *v* and a signing operation *m*^*s**modn.

We begin the attack with a bag of messages, all of them are valid, and we send them to the device under test (DUT). The DUT signs these messages (k messages), and for each one of the messages we get a trace, which is the data we collected using the side channel attack in this case it is only the time. Now we have a vector of size k and each element in the vector is the time it took to sign the message. Now, we are going to try and guess s_t, s_t − 1 (s=s_t,s_t − 1,s_t − 2,…,s₀) and try to discover s_t − 2.

So for each of the messages and each key guess we are going to simulate the computation as far as we already know and in addition for the parts of the key that we don’t know we are going to simulate twice - one with a 0 and one with a 1. We are going to find out where the extra reduction step happens. If the next bit is 0, then some of the messages have extra reduction and we classify the message into two bins, those who got extra reduction and those who didn’t. But maybe the key is not 0? maybe its 1. So we can simulate the same thing with the next bit as 1, and find out different set of messages with an extra reduction step. We can’t find what the bits are but we can make a guess and simulate on both 0 and 1. So, now we divide our traces into two groups in 2 different ways, if the next key bit is 0 then m₁, m₂, m₄, m₅, m₇ got extra reduction and m₃, m₆, m₈, m₉ didn’t. If the next key bit is 1 then m₂, m₃, m₅, m₈ got extra reduction and m₁, m₄, m₆, m₇, m₉ didn’t (see ).

If we guessed correctly what can we tell about the messages that got an extra reduction? Their runtime will be a little longer if we guessed the key bit correctly and If we guessed incorrectly it means we divided into two random groups which means the runtime will be similar in both groups. So if we guessed correctly the difference in runtime between the groups will be measurably different. So now we are going to change the discussion about the messages into the traces.

Guessing correctly the key bit makes the statics measurably different

if the next key bit is 0 then the statistics of the runtimes of 0 bit with extra reduction are going to be different from the runtimes of 0 bit without extra reduction. If we were wrong then the runtimes of 1 bit with extra reduction will be different from 1 bit without the extra reduction. Notice that we are not saying average or mean anywhere, because they are not required, it could be the variance changes or something else. The point is that there is some kind of difference that we can measure. So, how can we find out which of these two divisions is the correct one? Answer: we have two divisions of k traces and we measure the distance of the means. We are going to calculate the mean runtime of each part (0 bit with or without the extra reduction and 1 bit with or without the extra reduction) and subtract between with/without extra reduction in each bit guess. If there is a large distance of means of the 0 bit guess as oppose to the 1 bit guess then probably the splitting of traces in the 0 bit guess is more meaningful than the 1 bit guess. If we are able to split meaningfully then we guessed the key correctly. Now, let’s go back into statistics and talk about the T-test . The T-test was invented by William Sealy Gosset who was a chemist who worked for a very famous brewery in Ireland (Guinness). So, what is the idea? We have two populations that are different in some way. There are two kinds of t-tests, pair T-test and unpaired T-test. what is the paired T-test? lets assume we are going to a tree and we taking the leaves that fall off the tree. We notice that the leaves that fall on the south side have less mold that the leaves that fall on the north side. Why is that? Because there is more sun on the south side that is drying the leaves.

How do we prove our theory? We send our undergrad research assistant to collect a bag of leaves form the north side and a bag of leaves from the south side and tell the undergrad to count the percentage of mold in the southern and northern leaves. When the undergrad comes back, very exhausted, he provides us with an excel file that have 1000 leaves from the north side and 1500 from the south side. Now we want to prove our theory, each one of the leaves has a mold, We want to prove that there is a statistical difference between the two groups - this is the unpaired T-test. What is the paired T-test? It is when we are talking about something which we can identify as pairs. For example, we are developing a cancer medicine and we want to test it. Now, we don’t take any undergrads but only very sick mice with cancer. We measure the weight of the tumor in order to have a list of 100 mice and tumors. Then we divide them into two groups, one we treat with a medicine and the other we don’t. In the end of the experiment, we measure the tumors again, but now each measurement is a pair, one before the treatment and one is after. We want to say that the size of the tumor is smaller after the treatment. Now let’s review the student’s unpaired T-test demo in Matlab. The mat in Matlab is for matrix, we can define matrix like this:

The function randn(1) which creates normally distributed random variable which follows a Gaussian distribution which means the variance is 1 and the mean of 0. What is the minimum value this function will output? Answer: None, but statistically the value is closer to 0. How can we create a random variable with mean different from 0? Answer: add a constant to the mean, if we want mean N. we will do N + randn (1). We can even create a vector of randomly chosen numbers using randn (1, 5) + 5 : [4.9369, 5.7147, 4.7950, 4.8759, 6.4897] and if we will do randn (1, 5)*.1 + 5 the numbers will be even closer to 5. So, now we are ready to try the student T-test.

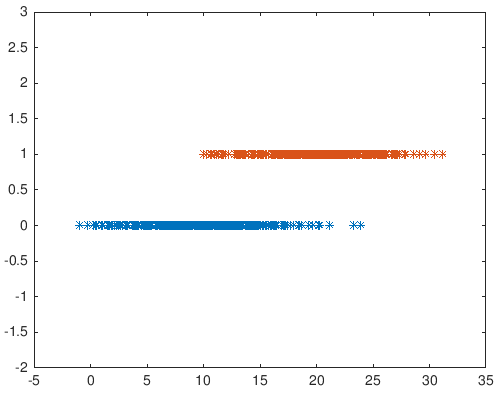
Plotting of the vectors for mu_1 = 10, mu_2 = 20 — Plotting of the vectors for mu₁ = 10, mu₂ = 20

Looking only on the graphs - can we say they are from the same distribution? Answer: we can’t be sure. We want to run the T-test to find out if they are statistically significant. There is a hypothesis and we need to either reject or accept the hypothesis. If H₀ then they are from the same distribution and if H₁ than they are from different distributions. If we run the code, the result will be that they are from different distributions with 0.959 certainty. Each time we run we can get different results, if the certainty is smaller than 0.95, the hypothesis is rejected. How can we make it more difficult for the ttest2? Answer: if we change m**u₂ to 11, then they will be very close distributions.

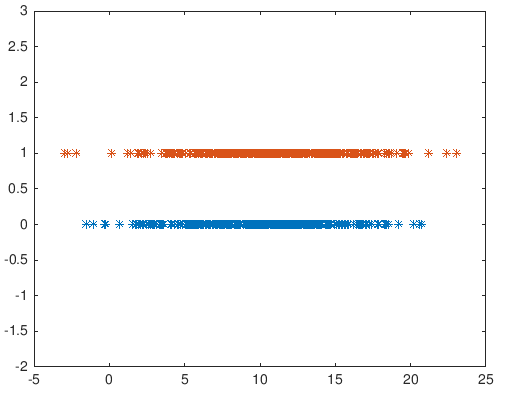
Plotting of the vectors for mu_1 = 10, mu_2 = 11 — Plotting of the vectors for mu₁ = 10, mu₂ = 11

How we as attackers can handle this situation? Answer: run many times. So we change the vector length (for example to 50000). There is something called power analysis, which means given these parameters (mu* and *sigm**a) how many measurements you need to run to be sure with 95 percent. As engineers we don’t really care about T-tests, we have a budget of measurements and we just take the one with the larger mean distance, but what if we are wrong (guessed 1 instead of 0)? After we guessed one bit wrong all the bits afterwards are wrong because they are simulated wrongly. So, how can we simulate a full attack? If we guessed 1 bit using the differences of means then we continue to the next bit in linear time. Let’s review a figure from “ A Practical Implementation of the Timing Attack” which you are encouraged to read.

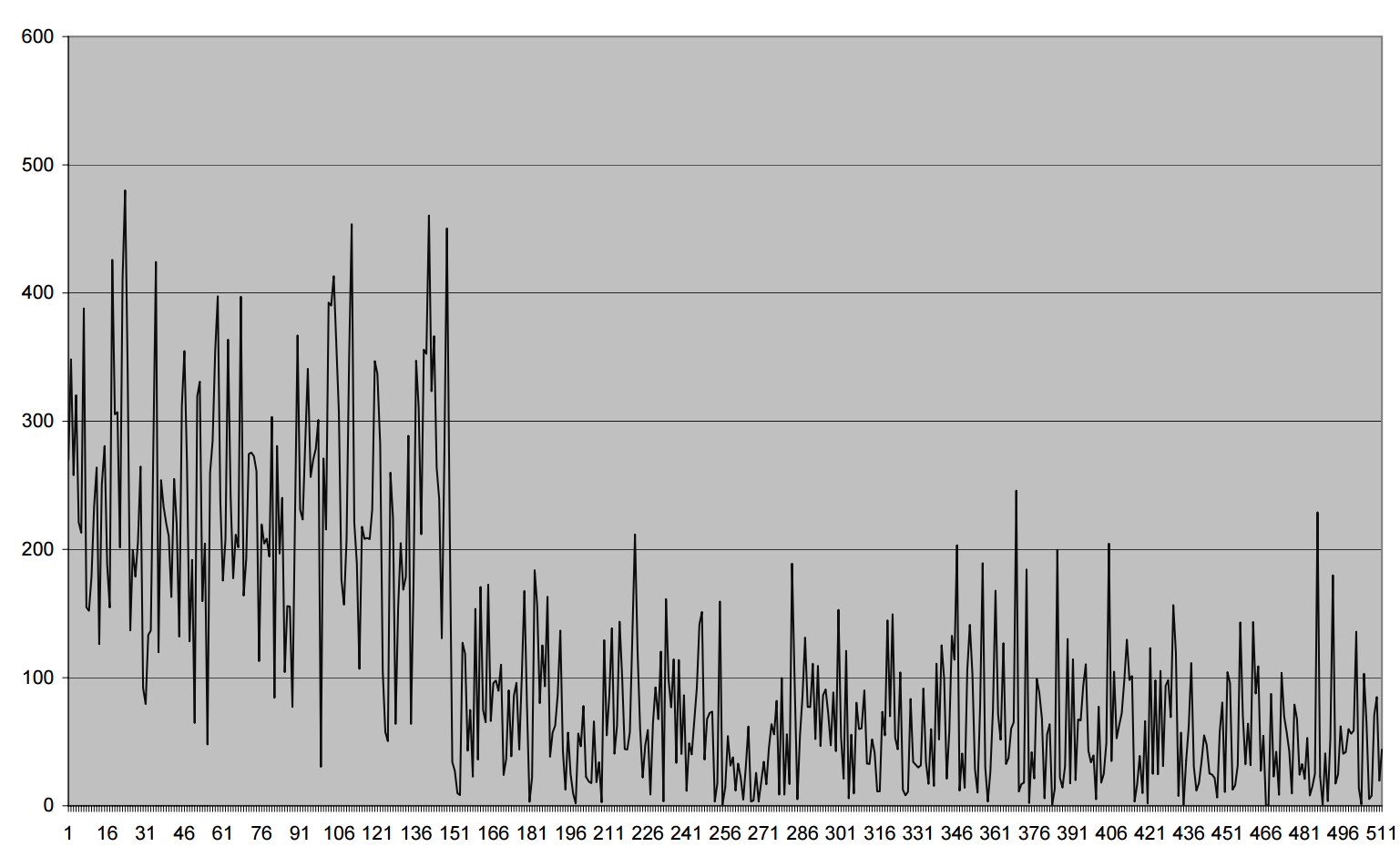
x axis – is the bit index from right to left (the left most bit is known to be 1) and y axis – is the distance of means we chose (some times its 500 or 100 but after 151 the distance of means is a lot smaller which means we guessed a bit wrong). How to solve it? Answer: go backwards and backtrack.

Now let’s talk about counter measurements. When Kocher announced the attack to the cypherpunks mailing list there was kind of discussion about it. Here is a message (see ) from there that was sent by Ron Rivest. He was replying to William Simpson, who was the author of Photuris which is related to the IPsec protocol and was used for key exchange in the IP protocol.

When he read that this attack can attack Photuris, Bill replied: don’t worry this will be fixed in Photuris. How to do this? By dithering the return time of identification message a few extra milliseconds. Which means he is doing mitigation, as he is not adding a random delay because random is very expensive, he is going to finish the calculations and is going to look at the clock and exactly when the millisecond changes (or second) send the package. What does it mean? It means that since the beginning is random then he is going to add a random delay. So, what Ron Rivest replied? It will reduce the data leakage but will not eliminate it. Why so? How the attacker will overcome this? He will need to measure more, this is network-based protocol, the attacker can measure as many times as he wants. He says, in addition, the public key computation time should be constant and independent from the message being sent. Ron Rivest suggest prevention as a countermeasure. So, what time it is going to be? Answer: the worst-case time. he adds a side note that this kind of attack is very difficult to mount in an internet environment due to packet-routing timing variabilities, however it is wise to be careful. Few years later a demonstration was presented over the internet, there were more measurements to counter the routing problem. Adding noise is sometimes the only thing that works, if you add enough noise to delay the attack time up to a year the message might not be relevant by the time the attack succeeds.

So, let’s talk about two more counter measurements, which are preventions. The first one is called RSA blinding. RSA blinding is a prevention counter measure which actually works on average time and not on worst-case time. if we have a secret key S and want to calculate m^smod**n, and the attacker gives us m and we don’t want to leak s. We showed that with enough attempts from the attacker he will eventually retrieve s.

So, how do we do blinding? First of all, we can do this even before the attacker arrives, we generate random r and calculate r^vmodn* and *r*⁻¹*modn. These calculations are not reviling any secrets because v is the public key. The attacker gives us m, so we calculate:

X = (r^v*m)modn* *Y* = *X*^*s* = (*r*^*v***m*)^*s* = *r*^*v**s* * *m*^*s* = *r* * *m*^*s**modn //v * smodn = 1mod**n)

Now, Y is leaking information because we raise a number to the power of the secret key, but r is a random number which the attacker doesn’t know so he can’t simulate the execution. How we remove r? We just calculate

S = Y * r⁻¹ = r * m^s * r⁻¹ = m^smod**n

Why doesn’t everybody use it? Answer: because it’s expensive, 2 modular exponentiations instead of 1. Another problem is the random number generation, its hard to find random number generator. You can see RSA blinding in openPGP.

Now let’s review another countermeasure. It called square and always multiply (see ). It is very similar to the square and multiply, just instead of only when d_i is 1 we will always calculate the multiply but the assignment will be only when d_i is 1. The problem with this is not the extra computation that came from turning sometimes to always. Speculative execution is always looking for instruction to execute, how does it decide if it will execute an instruction? If all it’s dependencies are met. If I say a = b * c and e = b * c they can run both in the same time. What happens is when the instruction brought to the CPU there is actually nobody is waiting for t, so as soon as it finishes to run the s = s * smodn and d_i is equal to 0 it will just return s. Moreover, the compilers are also capable of detecting such cases and optimize them by dismissing the else statement. So if we have a very simple CPU with no speculative execution no compiler and we wrote it in assembly we won’t be able to attack it, but we could use power analysis.

If we run this algorithm as is, we have two places in memory for s and for t, every action we load s then multiply and then edit the memory of s. Same goes in the multiply section. We load s and m and then multiply and store it in s. It’s always loading and storing s, but what happens when it goes to the else statement: it loads s and m and then store this into something other then s. So the power consumption is different between the store and the load. You can read more in the paper (“defeating RSA multiply-always and message binding” by Marc F. Witteman et al. )

Side channel attacks can get not only computer secrets but human secrets too. What exactly is a human secret? Browsing history for example. How does the website figure out our browsing history? Theoretically, we can delete the history in the browser. But what happens when we click on a hyper link (blue link)? It turns purple after the click. So, there was a nice trick that websites used to do, they attached the link to an HTML element and added JavaScript code that at the change of the color can now update that you have visited the site. The world wide web consortium decided that it was a privacy leak and you are not allowed to read the color of an HTML element anymore. Now we can set the color but can’t read it. One of the speakers in the black hat 2013 used timing attacks to find out if a web site was visited or not³. He also demonstrated how he can also use timing attack to read the user’s stream.

Research highlights

Photonic Side Channel Attacks Against RSA - This paper describes an attack utilizing the photonic side channel against a public-key crypto-system. They evaluated three common implementations of RSA modular exponentiation, all using the Karatsuba multiplication method. It was discovered that the key length had marginal impact on resilience to the attack. They noticed that the most dominant parameter impacting the attacker’s effort is the minimal block size at which the Karatsuba method reverts to naive multiplication. They also discovered that Montgomery’s Ladder was actually the most susceptible to the attack. Photonic Side Channel Attacks Against RSA.
Thermal Covert Channels on Multi-core Platforms - This paper demonstrates a way to leak information between 2 applications which are running on the same machine but with complete CPU core isolation or timing separation. The paper is presenting a way to bypass the first tactic by utilizing the heat factor and describing an attack where one CPU core is generating heat because of running a CPU intensive task (such as RSA decryption looped for 100 milliseconds) and the nearby CPU core picking up the heat as it propagates from the original core to its neighbors (by the laws of physics). The way to bypass the second type of isolation is just like the first one, but in this example the applications are not running at the same time. Still, the second application can track the remanent heat generated from the first application. The paper then offers a future work where an application can use these methods in combination with machine learning techniques to be able to learn the purpose of other applications running on the same machine without having the permissions to do so. Thermal Covert Channels on Multi-core Platforms.
Summarize of Drones’ Cryptanalysis -
Smashing Cryptography with a Flicker Paper This paper addresses the question how we can tell whether a passing drone is being used by its operator for a legitimate purpose (e.g., delivering pizza) or an illegitimate purpose (e.g., taking a peek at a person showering in his/her own house).

Over the years, many methods have been suggested to detect the presence of a drone in a specific location, however since populated areas are no longer off limits for drone flights, the previously suggested methods for detecting a privacy invasion attack are irrelevant.

In this paper, By applying a periodic physical stimulus on a target/victim being video streamed by a drone, a new method that can detect whether a specific POI (point of interest) is being video streamed by a drone is presented. Based on this method, an algorithm for detecting a privacy invasion attack is presented.
The paper analyse the performance of the algorithm using four commercial drones.

It show how the method that been suggested can be used to determine whether a detected FPV (first-person view) channel is being used to video stream a POI by a drone, and locate a spying drone in space.

The evaluation on algorithm that presented in the paper shows that a privacy invasion attack can be detected by the system in about 2-3 seconds.
Summarize of Whispers in the Hyper-space:
High-speed Covert Channel Attacks in the Clouds In the paper the authors are presenting the usage of two covert channels to communicate between two virtualized x86 systems that run on the same physical machine, they develop a robust communication protocol to deal with high noise in the covert channel and achieve information transfer of more than 100 bps with 0.75 The researchers went over the different x86 processors’ generations and showed that they can create a covert channel with each one, whether it contains a memory bus (new) or not (old). The first covert channel type they showed is based on using the bus lock mechanism. According to the implementation of an atomic instruction, the sender can lock the bus when using the instruction. locking the bus has effects over the whole system and the receiver can measure the latency when getting some variables and determine if 1 or 0 was sent by the receiver. The second covert channel type is using atomic instruction over two cache lines when no bus lock mechanism exists. The atomicity is achieved by flushing all inflight memory transactions from all cores which will result in observable latency. This work had shown how to solve three obstacles when creating a covert channel in the cloud, first memory addressing uncertainty- the sender and the receiver cannot know the exact cache locations of each other because they are located in different virtual environments with different memory mappings. Second process scheduling uncertainty - in classic cache covert channel the receiver runs after the sender (round-robin scheduling), but when the two processes located in different VMS, this scheduling is not guaranteed. Third physical limitation - processes of the receiver and sender may run on different cores and may not share caches L1 and L2.
Cross-Origin Pixel Stealing: Timing Attacks Using CSS Filters - In the paper , the authors present the following threat model: the attacker runs a malicious domain. His purpose is to tempt his victim to use the malicious domain. He either creates an interesting website to attract the victim to use it for a while,or he is able to open another window in front of the window being attacked.

Hypertext Markup Language (HTML) is the standard markup language for documents designed to be displayed in a web browser. The Document Object Model (DOM) is a cross-platform and language-independent interface that treats an XML or HTML document as a tree structure wherein each node is an object representing a part of the document. It is shown in the paper, how the rendering process of DOM content makes timing attacks possible: CSS filters allow styling of HTML components, CSS Custom filters (a.k.a shaders) have access to the rendering content, which can hold sensitive information, so an attack on shaders could lead to information leaks. But even without this access, different type of code parts in shaders could enable timing attacks.
1. Expand a single pixel - We need to choose which pixels we want to steal, and in each iteration of the attack we need to take only one pixel from the image and enlarge it, to be at the size of the whole screen in order to cancel the noise of all the other pixels and distinguish between only one black and white pixel. Worth mentioning that a method has been found to be able to find the exact character out of 16 digits by measuring the value of only 4 bytes, and in general character set of size N can be read by testing only log₂(N) pixels.
2. Framing a page - The attacker frames a website that has neglected to use X-Frame-Options.
3. The victim visits a malicious page - The victim visits the attacker’s malicious web page and is tricked into remaining on the page for the duration of the attack, e.g. by an interesting advertisement.
4. Traversing the page - Activate a combination of CSS filters over the page to convert each value to be RGB(0,0,0) - black, or RGB(255,255,255) - white.
5. Average framerate is captured - Using requestAnimationFrame to determine the average framerate on the browser window for each target pixel.
6. Interpreting the captured data - An array of pixel measurements are sent to the attacker’s server to be interpreted, The attacker can even build a classifier to determine the exact results based on the measurements.
As a result of this attack, and serval similar attacks discovered at the same time, all web browsers had changed their filters implementation to be without color-related optimization and all calculations are supposed to take the exact same time. Despite that, people are always finding new ways to steal pixels through other, creative, ways e.g. floating-point or hardware implementation of the CPU. And so, the fight for security is still ongoing to this day.

Division is the most expensive integer operation exists, and therefore we don’t want to do many divisions ↩
https://www.hackersdelight.org/MontgomeryMultiplication.pdf ↩
https://www.youtube.com/watch?v=KcOQfYlyIqw ↩